Creating a QMModel: Fitting the model
[1]:
import numpy as np
import ase
from ase.build import molecule
[2]:
from qmlearn.api.api4ase import QMLCalculator
from qmlearn.drivers.mol import QMMol
from qmlearn.io.hdf5 import DBHDF5
from qmlearn.model import QMModel
Open a Database
Import a database to get the reference molecule
refqmmol, the traning atomstrain_atoms, and the traning propertiesproperties.
[3]:
dbfile = 'h2o_vib_QML_set.hdf5'
db = DBHDF5(dbfile)
db.names
[3]:
['rks', 'rks/qmmol', 'rks/train_atoms_36', 'rks/train_props_36']
[4]:
db.get_names('*/train*')
[4]:
['rks/train_atoms_36', 'rks/train_props_36']
[5]:
refqmmol = db.read_qmmol(db.get_names('*/qmmol')[0])
train_atoms = db.read_images(db.get_names('*/train_atoms*')[0])
properties = db.read_properties(db.get_names('*/train_prop*')[0])
db.close()
Feature-Target definition
Define the feature, covariates or predictors by
X, and the label, target or responsey.
[6]:
X = properties['vext']
y = properties['gamma']
Call scikit-learn model
Define the scikit-learn model to fit
Xandy, in a a dictionary calledmmodels.
[7]:
from sklearn.kernel_ridge import KernelRidge
from sklearn.linear_model import LinearRegression
mmodels={
'gamma': KernelRidge(alpha=0.1,kernel='linear'),
'd_gamma': LinearRegression(),
'd_energy': LinearRegression(),
'd_forces': LinearRegression(),
}
Fitting
Creat the object
modeland fit it.
[8]:
model = QMModel(mmodels=mmodels, refqmmol = refqmmol)
[9]:
model.fit(X,y);
Creating a QMModel: Predicting with the model
Predicting gamma
Use
model.refqmmol.duplicateobject to initialize a specific geometry, as well as, define the shape of the external potentialvext, to be use ingamma.reshape.
[10]:
itest = 5
[11]:
qmmol=model.refqmmol.duplicate(train_atoms[itest])
[12]:
shape = qmmol.vext.shape
Predict gamma using
model.predictfunction.Use
qmmol.calc_etotalto use PySCF engine and predict the total energy based on the predictedgamma.Get the energy difference against the exact gamma using PySCF engine.
[13]:
gamma = model.predict(qmmol)
gamma = gamma.reshape(shape)
qmmol.calc_etotal(gamma)-properties['energy'][itest]
[13]:
-0.000498411246582009
Delta learning proccess
Rotate the predicted 1-RDM with respected to the reference geometry.
[14]:
gammas = []
for i, mol in enumerate(train_atoms):
dm = model.predict(mol, refatoms=mol).reshape(shape)
gammas.append(dm)
Do the delta learning proccess among
gammasand the ‘true’gamma,energyandforces.
[15]:
model.fit(gammas, properties['gamma'], method = 'd_gamma')
model.fit(gammas, properties['energy'], method = 'd_energy')
model.fit(gammas, properties['forces'], method = 'd_forces');
Check the energy difference against the exact gamma using PySCF engine.
[16]:
model.predict(gamma, method='d_energy')-properties['energy'][itest]
[16]:
2.6610933900883538e-08
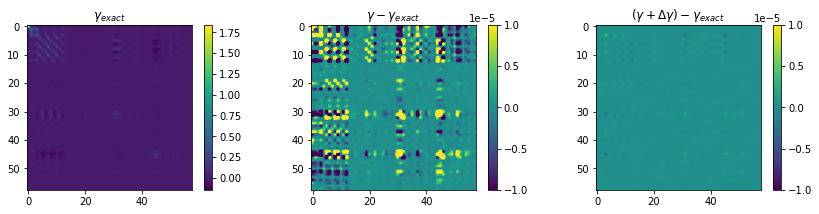
Plot the exact gamma \(\gamma_{exact}\), and its difference between the gamma from a first learning proccess \(\gamma-\gamma_{exact}\), and the delta learning gamma \((\gamma+\Delta\gamma)-\gamma_{exact}\) .
[17]:
gamma2 = model.predict(gamma, method='d_gamma').reshape(shape)
[18]:
gamma_exact= properties['gamma'][itest]
[19]:
import matplotlib.pyplot as plt
[20]:
fig, axs = plt.subplots(1,3, figsize=(12,3))
im0 = axs[0].imshow(gamma_exact)
im1 = axs[1].imshow(gamma-gamma_exact, vmin=-1E-5, vmax=1E-5)
im2 = axs[2].imshow(gamma2-gamma_exact, vmin=-1E-5, vmax=1E-5)
axs[0].set_title(r'$\gamma_{exact}$')
axs[1].set_title(r'$\gamma-\gamma_{exact}$')
axs[2].set_title(r'$(\gamma+\Delta\gamma)-\gamma_{exact}$')
plt.colorbar(im0, ax=axs[0])
plt.colorbar(im1, ax=axs[1])
plt.colorbar(im2, ax=axs[2])
fig.tight_layout()